AES 之Sub_Bytes&Mix_Columns（一）

Sub_Bytes（字节代换）：

AES的字节代换其实就是一个简单的查表操作。

AES的S盒，也称为字节替换（SubBytes）步骤中的Rijndael S盒，是一个复杂的结构。它是一个16x16的查找表，接受8位输入并产生8位输出。AES的S盒是通过将每个字节与其逆元素在有限域GF(2^8)上相乘，然后通过一个固定的仿射变换得到的。这个S盒不仅具有非线性，而且还具有很好的扩散特性，能够抵抗各种密码分析技术。

其设计过程如下：

• 逆元素：首先，对于有限域GF(2^8)中的每个非零元素，找到它的逆元素。在GF(2^8)中，每个非零元素都有一个唯一的逆元素，使得它们的乘积模x^8 + x^4 + x^3 + x + 1等于1。
• 仿射变换：接下来，对每个逆元素应用一个仿射变换。这个变换由一个可逆的线性变换和一个非线性变换组成，非线性变换是通过将每个字节与一个固定的多项式在GF(2^8)上相乘来实现的。
• 优化：最后，对S盒进行优化，以确保它满足上述安全原则。这可能包括调整仿射变换的参数，以确保S盒对于各种密码分析技术具有足够的抵抗能力。

S盒定义：

行/列	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0x63	0x7c	0x77	0x7b	0xf2	0x6b	0x6f	0xc5	0x30	0x01	0x67	0x2b	0xfe	0xd7	0xab	0x76
1	0xca	0x82	0xc9	0x7d	0xfa	0x59	0x47	0xf0	0xad	0xd4	0xa2	0xaf	0x9c	0xa4	0x72	0xc0
2	0xb7	0xfd	0x93	0x26	0x36	0x3f	0xf7	0xcc	0x34	0xa5	0xe5	0xf1	0x71	0xd8	0x31	0x15
3	0x04	0xc7	0x23	0xc3	0x18	0x96	0x05	0x9a	0x07	0x12	0x80	0xe2	0xeb	0x27	0xb2	0x75
4	0x09	0x83	0x2c	0x1a	0x1b	0x6e	0x5a	0xa0	0x52	0x3b	0xd6	0xb3	0x29	0xe3	0x2f	0x84
5	0x53	0xd1	0x00	0xed	0x20	0xfc	0xb1	0x5b	0x6a	0xcb	0xbe	0x39	0x4a	0x4c	0x58	0xcf
6	0xd0	0xef	0xaa	0xfb	0x43	0x4d	0x33	0x85	0x45	0xf9	0x02	0x7f	0x50	0x3c	0x9f	0xa8
7	0x51	0xa3	0x40	0x8f	0x92	0x9d	0x38	0xf5	0xbc	0xb6	0xda	0x21	0x10	0xff	0xf3	0xd2
8	0xcd	0x0c	0x13	0xec	0x5f	0x97	0x44	0x17	0xc4	0xa7	0x7e	0x3d	0x64	0x5d	0x19	0x73
9	0x60	0x81	0x4f	0xdc	0x22	0x2a	0x90	0x88	0x46	0xee	0xb8	0x14	0xde	0x5e	0x0b	0xdb
A	0xe0	0x32	0x3a	0x0a	0x49	0x06	0x24	0x5c	0xc2	0xd3	0xac	0x62	0x91	0x95	0xe4	0x79
B	0xe7	0xc8	0x37	0x6d	0x8d	0xd5	0x4e	0xa9	0x6c	0x56	0xf4	0xea	0x65	0x7a	0xae	0x08
C	0xba	0x78	0x25	0x2e	0x1c	0xa6	0xb4	0xc6	0xe8	0xdd	0x74	0x1f	0x4b	0xbd	0x8b	0x8a
D	0x70	0x3e	0xb5	0x66	0x48	0x03	0xf6	0x0e	0x61	0x35	0x57	0xb9	0x86	0xc1	0x1d	0x9e
E	0xe1	0xf8	0x98	0x11	0x69	0xd9	0x8e	0x94	0x9b	0x1e	0x87	0xe9	0xce	0x55	0x28	0xdf
F	0x8c	0xa1	0x89	0x0d	0xbf	0xe6	0x42	0x68	0x41	0x99	0x2d	0x0f	0xb0	0x54	0xbb	0x16

状态矩阵中的元素按照下面的方式映射为一个新的字节：把该字节的高4位作为行值，低4位作为列值，取出S盒或者逆S盒中对应的行的元素作为输出。
例如:
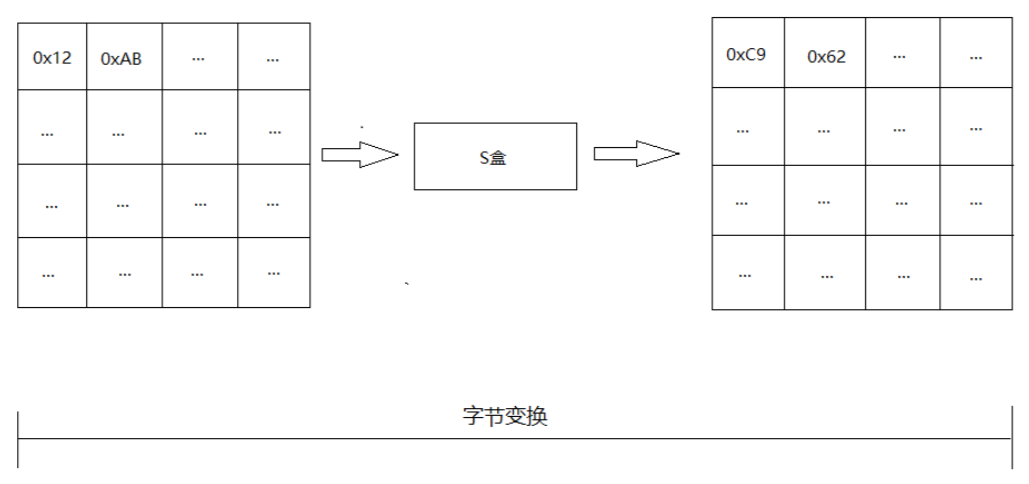
加密时输出的字节S1为0x12,则查S盒的第0x01行和0x02列，得到值0xc9,然后替换S1原有的0x12为0xc9；
加密时输出的字节S4为0xAB,则查S盒的第0x0A行和0x0B列，得到值0x62,然后替换S4原有的0xAB为0x62。

状态矩阵经字节代换后的图如下：

代码实现：

def sub_bytes(state):
    """
    使用S盒对状态矩阵进行字节代换操作。

    参数：
        state: 4x4矩阵，表示状态

    返回值：
        无，直接修改原始状态矩阵
    """
    for i in range(4):
        for j in range(4):
            byte = state[i][j]
            row = (byte & 0xF0) >> 4
            col = byte & 0x0F
            state[i][j] = sbox[row][col]

Mix_Columns（列混合）：

列混合变换是通过矩阵相乘来实现的，经行移位后的状态矩阵与固定的矩阵相乘，得到混淆后的状态矩阵，如下图的公式所示：

状态矩阵中的第j列(0 ≤j≤3)的列混合可以表示为下图所示：

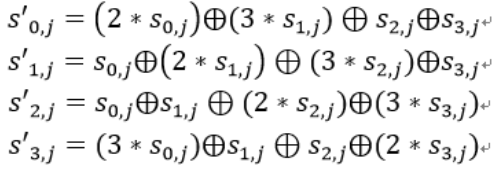
列混合数学基础：

矩阵乘法在AES的有限域GF(2^8)上进行，这意味着加法和乘法都是在模数为x^8 + x^4 + x^3 + x + 1的有限域中进行的。

加法：等价于两个字节的异或；

乘法：两元素多项式相乘，模m(x)；

例：57×83=C1

(x^6+x^4+x^2+x+1)*(x^7+x+1)=x^7+x^6+1 mod m(x)

AES算法中定义m(x)多项式（不可约多项式）为：m(x)=x^8+x^4+x^3+x+1（十六进制的011B)

简化理解：

对于一个8位的二进制数来说，使用域上的乘法乘以0x02(00000010)等价于左移1位(低位补0)后，再根据情况同固定的数0x1B(00011011)进行异或运算。如果a7为1，则进行异或运算，否则不进行。

设S1 = (a7 a6 a5 a4 a3 a2 a1 a0)，则0x02 * S1如下图所示：

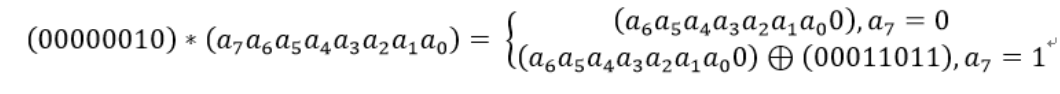
结合律：类似地，乘以(00000100)可以拆分成两次乘以(00000010)的运算：

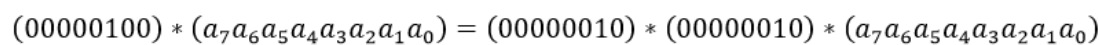
结合律：乘以(0000 0011)可以拆分成先分别乘以(0000 0001)和(0000 0010)，再将两个乘积异或：

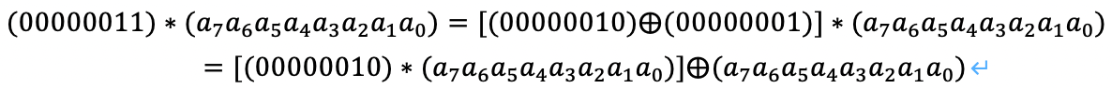
代码实现：

def galois_mult(a, b):
    # GF(2^8)上的有限域乘法
    p = 0
    for i in range(8):
        if b & 1:
            p ^= a
        high_bit_set = a & 0x80
        a <<= 1
        if high_bit_set:
            a ^= 0x1B  # x^8 + x^4 + x^3 + x^1 + x^0
        b >>= 1
    return p & 0xFF


def mix_columns(state):
    """
    对状态矩阵进行列混合操作。

    参数：
        state: 4x4矩阵，表示状态

    返回值：
        无，直接修改原始状态矩阵
    """
    new_state = [[0] * 4 for _ in range(4)]
    for c in range(4):
        for r in range(4):
            new_state[r][c] = (
                    galois_mult(state[0][c], mix_columns_matrix[r][0]) ^  # 第一列的乘法
                    galois_mult(state[1][c], mix_columns_matrix[r][1]) ^  # 第二列的乘法
                    galois_mult(state[2][c], mix_columns_matrix[r][2]) ^  # 第三列的乘法
                    galois_mult(state[3][c], mix_columns_matrix[r][3])  # 第四列的乘法
            )
    for r in range(4):
        for c in range(4):
            state[r][c] = new_state[r][c]