RSA

本文最后更新于：2024年7月2日 下午

公钥密码体制

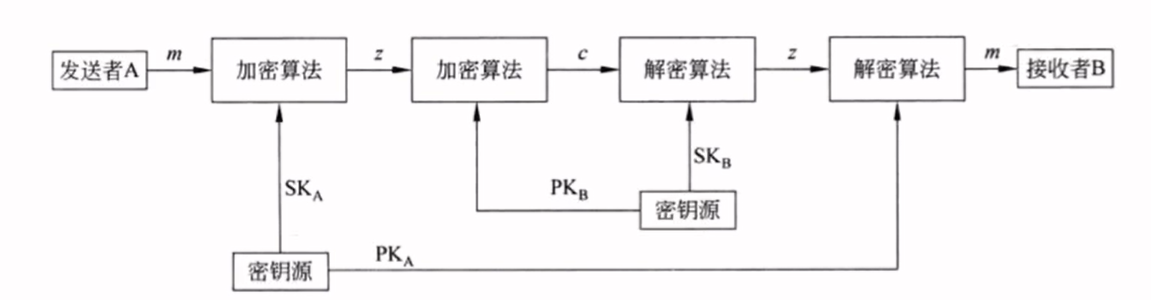
保密 + 认证

RSA

RSA算法是一种非对称加密算法，由Ron Rivest、Adi Shamir和Leonard Adleman于1977年发明，并以他们的姓氏首字母命名。RSA算法基于大数分解的难题，即分解两个大素数乘积的难度，这是RSA算法的安全基础。

主要步骤

1.密钥生成

  • 选择两个大质数p和q。
  • 计算n = p * q，n是加密密钥。
  • 计算欧拉函数φ(n) = (p-1) * (q-1)。
  • 选择一个小于φ(n)的整数e，使得e和φ(n)互质（即它们的最大公约数为1）。
  • 计算d，使得e * d ≡ 1 (mod φ(n))。d是解密密钥。

2.密钥分发

  • 公开n和e，作为公钥。
  • 保密d，作为私钥。

3.加密

  • 使用公钥（n和e）进行加密。
  • 选择明文消息m（0 < m < n）。
  • 计算密文c = m^e (mod n)。

4.解密

  • 使用私钥（n和d）进行解密。
  • 计算明文m = c^d (mod n)。

素性检验

试除法

（Trial Division）是一种简单但效率较低的素数检验方法。它通过尝试将给定的数n除以所有小于等于n的质数来判断n是否为素数。如果n可以被任何一个这样的质数整除，那么n就不是素数。如果n不能被任何一个这样的质数整除，那么n可能是素数。
试除法的步骤如下：

  1. 选择一个质数p，p可以是从2开始的任意质数。
  2. 计算n除以p的余数r。
  3. 如果r等于0，则n不是素数。
  4. 如果r不等于0，选择下一个质数p+1，重复步骤2和3。
  5. 如果对所有小于等于√n的质数p，n都不能被整除，那么n可能是素数。

这种方法的时间复杂度是O(n^1/2)，因为它需要尝试所有小于等于√n的质数。因此，对于非常大的数，试除法非常慢。此外，试除法对于某些合数可能会产生假阳性，即错误地判断合数为素数。
在实际应用中，试除法通常用于较小的数或者作为其他更高效素性检验方法的辅助。对于较大的数，通常会使用米勒-拉宾素性检验等更高效的概率性方法。

示例
1
2
3
4
5
6
7
8
9
10
11
12
def is_prime(n):
    if n <= 1:
        return False
    if n <= 3:
        return True
    if n % 2 == 0:
        return False
    # 检查n是否为合数
    for i in range(3, int(n**0.5) + 1, 2):
        if n % i == 0:
            return False
    return True

在这个例子中，is_prime函数用于执行试除法。它首先检查n是否小于等于1，如果是，则返回False。然后，它检查n是否小于等于3，如果是，则返回True。接下来，它检查n是否可以被2整除，如果是，则返回False。最后，它通过循环检查n是否可以被所有小于等于n的奇数整除。如果n不能被任何一个这样的数整除，那么它可能是素数。

米勒-拉宾素性检验

（Miller-Rabin Primality Test）是一种概率性素性检验算法，用于判断一个数是否为素数。该算法基于一个称为费马小定理的数学原理，并经过优化，使其具有较高的效率和较低的错误率。
米勒-拉宾素性检验的基本步骤如下：

  1. 选择一个随机数a，a是2到n-2之间的整数。
  2. 计算r = n - 1，然后找到r的欧几里得算法除数d，满足d * 2^r ≡ 1 (mod n)。
  3. 计算x = a^d (mod n)。
  4. 如果x = 1或x = n-1，则n可能是素数。
  5. 对于k = 0到s-1，执行以下步骤：
    • 将r除以2，得到r_i = r / 2^i。
    • 计算x = x^2 (mod n)。
    • 如果x = 1，则n是合数。
    • 如果x = n-1，则继续下一次迭代。
    • 如果x^r_i ≡ -1 (mod n)，则n是合数。
  6. 如果所有迭代都没有发现n是合数，则n是素数。
    其中，s是测试的迭代次数，s越大，错误率越低。
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def miller_rabin_primality_check(n, k=20):
   """
   米勒-拉宾素性检验
   由于假设n是一个素数，n-1=a^s*d,s和d是常量，改变a的值，检测20次
   :param n:
   :param k:
   :return:
   """
   assert n > 3
   if n % 2 == 0:
       return False
   # 找出n-1 = 2^s*d
   s, d = 0, n - 1
   while d % 2 == 0:
       d >>= 1
       s += 1

   for _ in range(k):
       a = randrange(2, n - 1)
       x = pow(a, d, n)

       if x == 1 or x == n - 1:
           continue

       for _ in range(s):
           x = pow(x, 2, n)
           if x == n - 1:
               break
       else:
           return False
   return True

在这个例子中，miller_rabin函数用于执行米勒-拉宾素性检验。我们选择了一个随机数a，并进行了s次迭代。如果n通过了所有迭代，则我们认为是素数。如果n没有通过所有迭代，我们仍然不能确定它是合数，因为我们使用的是概率性测试。

快速模幂算法

（Fast Modular Exponentiation）是一种用于计算大数模幂运算的算法，其时间复杂度为O(log n)，其中n是指数的大小。这种算法特别适用于RSA加密算法中的密钥生成和加密过程。

快速模幂算法的基本思想是将指数n分解为二进制形式，并利用模运算的性质来简化计算。

具体步骤如下：

  1. 初始化：
    • 设置结果 result = 1。
    • 设置底数 base = base。
    • 设置模数 modulus = modulus。
  2. 二进制分解：
    • 将指数n转换为二进制形式，并计算其长度 bit_length = len(bin(n)) - 2。
  3. 循环计算：
    • 循环 i = 0 到 bit_length - 1。
    • 在每次迭代中，将 result 乘以 result（即 result = result * result mod modulus）。
    • 如果 n & (1 << i) 等于1（即二进制位的值为1），则将 base 乘以 result（即 result = base * result mod modulus）。
  4. 返回结果：
    • 循环结束后，result 将是 base^n mod modulus 的结果。
      快速模幂算法的一个关键优化是使用模平方来减少乘法运算。这样可以避免在每次迭代中都需要进行乘法运算，从而显著提高算法的效率。
示例
1
2
3
4
5
6
7
8
def fast_mod_pow(base, exponent, modulus):
    result = 1
    while exponent > 0:
        if exponent & 1:
            result = (result * base) % modulus
        base = (base * base) % modulus
        exponent >>= 1  # 右移一位，相当于除以2
    return result

在这个例子中，fast_mod_pow函数用于计算 base^exponent mod modulus。我们首先将指数转换为二进制形式，然后使用循环和模平方来计算结果。最后，我们打印出计算结果。

扩展欧几里得算法

扩展欧几里得算法（Extended Euclidean Algorithm）是欧几里得算法的一个变体，它不仅找到两个整数a和b的最大公约数gcd(a, b)，还找到一组整数x和y，使得等式ax + by = gcd(a, b)成立。这组整数x和y被称为扩展欧几里得算法的解。
扩展欧几里得算法的基本步骤如下：

  1. 如果a等于0，那么gcd(a, b)就是b，x是0，y是1。
  2. 如果b等于0，那么gcd(a, b)就是a，x是1，y是0。
  3. 否则，计算gcd(b, a % b)，并设x1、y1为x和y的值。
  4. 设置新的a为原来的b，新的b为x1，新的x为y1，新的y为x - (a // b) * y1。
  5. 重复步骤3和4，直到b为0。

扩展欧几里得算法的时间复杂度是O(log(min(a, b)))，因为每一步都减半了b的大小。

示例
1
2
3
4
5
6
7
8
def extended_euclidean(a, b):
    if a == 0:
        return b, 0, 1
    else:
        gcd, x1, y1 = extended_euclidean(b % a, a)
        x = y1 - (b // a) * x1
        y = x1
        return gcd, x, y

在这个例子中，extended_euclidean函数用于计算 gcd(a, b) 以及满足等式 ax + by = gcd(a, b) 的整数x和y。我们首先检查a是否等于0，如果是，则返回b和相应的x、y值。否则，我们递归地调用扩展欧几里得算法，直到b为0。最后，我们打印出gcd、x和y的值。

RSA代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
import math
from random import randrange

def generate_n_bit_odd(n: int):
   """
   生成大数,不确定是不是素数
   :param n:
   :return:大数
   """
   assert n > 1
   return randrange(2 ** (n - 1) + 1, 2 ** n, 2)


first_50_primes = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
                  37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
                  79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
                  131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
                  181, 191, 193, 197, 199, 211, 223, 227, 229, 233]

def get_lowlevel_prime(n):
   """
   选择满足不能够整除前50个素数的大数，没找到就一直循环
   :param n:
   :return:
   """
   while True:
       c = generate_n_bit_odd(n)
       for divisor in first_50_primes:
           if c % divisor == 0 and divisor ** 2 <= c:
               break
       return c


def miller_rabin_primality_check(n, k=20):
   """
   米勒-拉宾素性检验
   由于假设n是一个素数，n-1=a^s*d,s和d是常量，改变a的值，检测20次
   :param n:
   :param k:
   :return:
   """
   assert n > 3
   if n % 2 == 0:
       return False
   # 找出n-1 = 2^s*d
   s, d = 0, n - 1
   while d % 2 == 0:
       d >>= 1
       s += 1

   for _ in range(k):
       a = randrange(2, n - 1)
       x = pow(a, d, n)

       if x == 1 or x == n - 1:
           continue

       for _ in range(s):
           x = pow(x, 2, n)
           if x == n - 1:
               break
       else:
           return False
   return True


def get_random_prime(num_bits):
   """
   获取大素数
   :param num_bits:
   :return:
   """
   while True:
       pp = get_lowlevel_prime(num_bits)
       if miller_rabin_primality_check(pp):
           return pp


def gcd(a, b):
   """
   求最大公约数
   :param a:
   :param b:
   :return:
   """
   while b:
       a, b = b, a % b
   return a


def lcm(a, b):
   """
   求最大公倍数
   两个数的乘积等于它们的最大公约数和最小公倍数的乘积。
   """
   return a // gcd(a, b) * b



def exgcd(a, b):
    if a == 0:
        return b, 0, 1
    else:
        gcd, x1, y1 = exgcd(b % a, a)
        x = y1 - (b // a) * x1
        y = x1
        return gcd, x, y

def invmod(e, m):
   """
   求模逆元：知道x * e + y * m = g
   :param e:
   :param m:
   :return:
   """
   g, d, y = exgcd(e, m)
   assert g == 1
   if d < 0:
       d += m
   return d


def uint_from_bytes(xbytes: bytes) -> int:
   """
   比特转换位整数
   :param xbytes:
   :return:
   """
   return int.from_bytes(xbytes, 'big')


def uint_to_bytes(x: int) -> bytes:
   """
   整数转换成比特的时候，一个整数对应32位比特数
   :param x:
   :return:
   """
   if x == 0:
       return bytes(1)
   return x.to_bytes((x.bit_length() + 7) // 8, 'big')  #做到尽量不补零


RSA_DEFAULT_EXPONENT = 65537
RSA_DEFAULT_MODULUS_LEN = 2048

class RSA:
   """
   RSA算法(self.n, self.e)加密密钥
   (self.n, self.d)解密密钥
   """
   def __init__(self, key_length=RSA_DEFAULT_MODULUS_LEN,
                exponent=RSA_DEFAULT_EXPONENT):
       self.e = exponent
       t = 0
       p = q = 2  # 找出一个e使1<e<(p-1)*(q-1)
       while gcd(self.e, t) != 1:
           p = get_random_prime(key_length // 2)
           q = get_random_prime(key_length // 2)
           t = lcm(p - 1, q - 1)

       self.n = p * q
       self.d = invmod(self.e, t)  # 加密和解密使比特和整数之间的加解密

   def encrypt(self, binary_data: bytes):
       int_data = uint_from_bytes(binary_data)
       return pow(int_data, self.e, self.n)

   def decrypt(self, encrypted_int_data: int):
       int_data = pow(encrypted_int_data, self.d, self.n)
       return uint_to_bytes(int_data)


if __name__ == '__main__':
   RSA_1 = RSA(2048, 65537)
   msg = b'Complex RSA in Python'
   ctxt = RSA_1.encrypt(msg)
   m = RSA_1.decrypt(ctxt)
   print(m)
   print(ctxt)

密码学
#RSA
RSA
https://forever0823.github.io/2024/05/04/RSA/
作者
Alan
发布于
2024年5月4日
许可协议